Ⅱ.历法基础
二、太阳历与太阴历
我们在(一)中反复强调过一个便于计量和观察的天文系统对于历法编排的巨大便利性。事实上,在人类发明出均匀的时间计量系统之前,曾涌现出大量的历法,但大多数都在后人的观测中被证明是不精确的因而废止。其中只有少数经过精确的定义和不断改进才得以使用至今。前文所述的岁星纪年法就是因为木星存在逆行与超辰现象而无法准确地描述年度变化,最终于东汉时期被废止,改用《四分历》,采用干支纪年。
总的来说,大部分历法只以一种天体为制历标准,或观阳之节律(即太阳历),或查察月之圆缺(即太阴历)。中国农历独树一帜,它以一个回归年为别年标准,但划分月份时却是以月相变化为基础置月首,此称阴阳历。(所以把农历称为阴历是!一!种!错!误!叫!法!)
那么为什么要分太阳历和太阴历呢?首先想到的就是分别只考虑两者而形成的历法周期不同,既然周期不同,自然就无法把二者合而等之。事实上,历法对精确拟合气候变化和精确拟合月相变化的取舍程度不同,是导致历法分化的本质原因。
①太阳历
顾名思义,太阳历就是重视拟合气候变化甚于月相变化的历法。
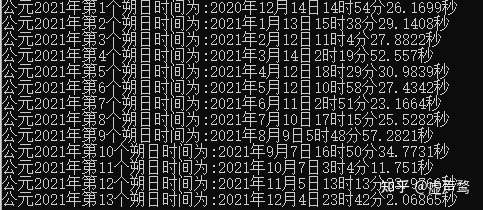
用天文方法计算出公元2021年的朔日时刻。我们可以显而易见地发现公历和月相变化周期完全不能建立任何联系。

回归年:指太阳中心连续两次通过春分点的时间间隔。(常用于历法计算)
恒星年:地球绕太阳公转360度的时间间隔。(常用于天文计算)
本来上述两个概念应该是等价的。但由于地球自转过程中地轴的进动运动,赤道平面会随之发生改变,造成春分点在黄道上由东向西移动,进而连续两次通过春分点时,太阳在不到一个恒星年的时间里就再次到达春分点。所以回归年比恒星年略短。
上述现象被简明表示为岁差。
在历法计算中,我们所称的年都是回归年。因为相较于旋转360度而言,寒暑周期的变化更为重要。
朔望月:月相每两次圆或缺之间相隔的时间(圆称"望"而缺称"朔")。
粗略地说,,这意味着1年(下文无特殊指出均指代回归年)大约能容纳下12个朔望月,这也是公历一年置12个月的原因。
以上所述的回归年周期与朔望月周期都是一段时间内的平均值,而实际值会在这个数值周围作小幅波动。
以回归年周期为重心考虑,如果每1年置12个朔望月,自然每隔大概3年就要面临多出1个月的问题。而朔望月的周期也是不固定的,再次给制定历法带来了困难,因此只能牺牲掉刻画月相变化的朔望月,改用别的方法定义"月"。
世界上实行过的太阳历主要有儒略历(Julian Calendar)与格里高利历(Gregorian Calendar)。
儒略历,是由罗马共和国独裁官儒略·凯撒采纳埃及亚历山大的数学家兼天文学家索西琴尼的计算后,于公元前45年1月1日起执行的取代旧罗马历法的一种历法。儒略历中,一年被划分为12个月,大小月交替;四年一闰,平年365日,闰年366日为在当年二月底增加一闰日,年平均长度为365.25日。
因此儒略历的置闰满足:!(y mod 4) (其中y为儒略历年,mod为取余运算)
考虑一个回归年的真实周期约为365.2422日,那么每过一年,儒略历就会比实际情况慢约0.0078日。如此累计,当此历法采用此历法沿用1600年时,累计误差将达到-12.48天,在缺少修正的情况下,儒略历的误差是不可接受的。
到1582年时,儒略历的春分日(3月21日)与地球公转到春分点的实际时间已相差10天。

因此,一种更合乎太阳运行规律的历法亟待被创造出来,这种出于此动机被创造出来的新历法就叫作格里高利历(格里历)。
格里历与儒略历大致一样,但格里历特别规定,除非能被400整除,所有的世纪年(能被100整除)都不设闰日;如此,每四百年,格里历仅有97个闰年,比儒略历减少3个闰年。格里历的历年平均长度为365.2425日,接近平均回归年的365.242199074日,即约每3300年误差一日,也更接近回归年的365.24237日,即约每8000年误差一日。格里历开始实行时,将儒略历1582年10月4日星期四的次日,设为格里历1582年10月15日星期五,即有10天被删除,但原星期的周期保持不变。
因此格里历的置闰满足:(! ( y mod 4 )&& y mod 100 ) ||(!(y mod 400 ) )
(其中&&表示逻辑与,||表示逻辑或)
上述表达式的书写并非不可调换顺序。但由逻辑短路原理,考虑到平凡年份(不是整百年也不是整四百年的年份)远远多于非平凡年份,并且整数为4的倍数是整数为100或400的倍数的必要条件,
故若要判定一年闰与否,应先判断年份与4的倍数关系,再判断其与100的倍数关系,若满足是4的倍数却不是100的倍数,辄闰。进而再判断是否为400的倍数,满足才闰。因为上述两种情况不可能同时出现,故用或连接。
格里历即为我们今天使用的公历。除却历法本身的自然科学意义(太阳历)外,格里历还具有相当浓厚的社会科学色彩,它以耶稣诞生为公元元年。全国政协第一届全体会议会上,与会人一致认为,应采用现代世界大多数国家公用的纪年制度,即用西元(公元)为新中国的纪年。
②太阴历
与①恰好相反,太阴历专注于刻画月相变化周期,而对气候的变化无从入手。
现行的阴历相对来说较少,这里权且尝试对阴历代表伊斯兰历做一些抛砖引玉的释读。
伊斯兰教历以月亮圆缺一周(朔望月)为一月,历时29日12小时44分2.8秒,月亮圆缺十二周为一年,历时354日8小时48分33.6秒。单数月份即1、3、5、7、9、11月为大建即大月,30天; 双数月份即2、4、6、8、10月为小建即小月,29天;12月平年为小建即29天,闰年为大建即30天。伊斯兰历以30年为一周期,每一周期的第2、5、7、10、13、16、18、21、24、26、29年,共11年为闰年,另19年为平年。伊斯兰教历对昼夜的计算,以日落为一天之始,到次日日落为一日,通常称为夜行前,即黑夜在前,白昼在后,构成一天,与公历农历都不同。从月的精度来看,伊斯兰教历迄今1400年间,朔日时刻仅比实际时刻落后半天,其精度与通用的公历相仿。只是因为增加闰月违反教义,伊斯兰历才始终保持其纯阴历状态。
为什么说伊斯兰历是纯阴历呢?如下图所示:
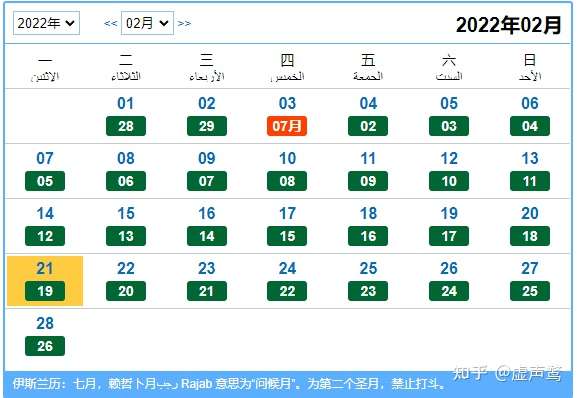
在人们的固有印象里,公历二月下旬比春分日还要早快一个月,自然是和七月暑气蒸腾之时扯不上半分关系的。然而伊历的编排方法却真真实实地导致了这种现象。
仔细阅读其编排规则不难发现原因所在。首先,它将一年简单地编为十二个月,考虑到一个朔望月的周期大约是29天半,因此从理论上说一半的月份定为29天,另一半定为30天是最简单的制定方法。事实上伊历也确实是这么做的。
然而这会带来一个问题,以一个朔望月的期望周期×12个月得出一个朔望年的长度约为354日8小时48分33.6秒,而一个回归年的长度约为365天5小时48分45.1秒,意味着一个朔望年是无法和一个回归年对齐的。另外出于宗教原因(伊历无闰月),这种误差无法及时地得到周期性修正,因此伊斯兰历在习惯把历法与物候挂钩的人眼中是可笑的。
但历法是便于人们纪元而创造出来的,不存在孰优孰劣之分,符合实际情况的就是最优解。
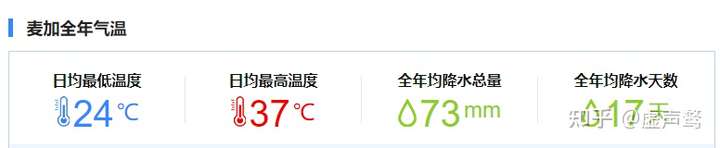
在终年炎热降水稀少的中东,随时间推移物候的改变并不明显。因此对于阿拉伯人来说,要采纳阳历这种历法与物候挂钩的模式反而是难以理解的。
三、农历(阴阳合历)
通过对阳历和阴历的简单认识,现在我们已经能认识到这两种纪元方法各自的优势和不足。
想象一下,对于一个位于北半球中纬,气候受季风影响比较显著的地区,应如何制定一种历法来指导广义的农业生产呢?如果是传统的种植业,似乎直接用阳历并无不妥。以夏至日举例,虽然每一年的夏至并不总落在公历的6月22日内,但因为阳历本身用于刻画物候变化,不存在像伊斯兰历一样每年都会累积误差的问题,故实际上夏至日的准确时刻可以看作是在期望时刻两边均匀分布的,这个规律同样适用于二分二至日的其他三个。(事实上如果我们对太阳的每个视黄经都安排一个节日庆祝,那么每个对应的节日的年间差异也极小)
然而渔业还需要考虑潮汐的涨落,而这是和地球所受引力存在密切关系的。随时间的推移,太阳与月球对地球引力的合力在持续变化,但这个变化并非无规律可循,它随地-月-日系统中三个星体的相对位置关系的改变而改变。(合力大小方向的变化有周期性)因而从观察月相的变化,我们就能推知潮汐可能的变化情况。
譬如当新月时(朔日),三者位于同一直线上且月日在地球的同侧,引力在同方向叠加。这时涨潮时容易形成大潮,在这一天选择出海捕鱼就是极其不明智的。
另外,人的生理周期与月相变化也有一定的关系。中医学讲求因时制宜,若能根据月相周期进行治疗方案的修正,想必也是极好之事。
最后,在中国传统宗教道教中,朔望两天常被赋予非凡的意义,某些宗教仪式常会在这两天进行。
综上所述,创造出一种兼有阳历又有阴历优点的历法需求就呼之欲出了。农历的出现,完美地解决了这个需求,为农业生产提供了可靠性极佳的参考依据。
想一手抓月亮圆缺一手抓气候变化,把两者视为等同的绮想显然是不合理的,我们肯定得有所偏私。那么要如何更合理地定义年和月呢?
农历的解决方案是:把从一个冬至日起,到下一个冬至日为止的这段时间称为一岁,而一年的开始取决于月建,与一岁并不是相同的概念。农历规定冬至日必须落在子月,那么十二地支中的其他十一支,可以与余下的十一个月一一相配,这样每个月就都有特定的称谓了。
为了厘清岁与年的区别,我们必须先引入一个额外内容:
1.月建
在固定位置的某一特定时间观察,北斗七星斗柄所指方向即为月令,而一年的第一个月令称为月建。
北斗星分别按年按日遍历十二宫,所历一年之春、夏、秋、冬四季,与一日之晨、午、昏、夜,行度相符,即以斗纲所建,春行寅、卯、辰宫,夏行巳、午、未宫,秋行申、酉、戌宫,冬行亥、子、丑宫;一日则晨行寅、卯、辰宫,午行巳、午、未宫,昏行申、酉、戌宫,夜行亥、子、丑宫。是以对照行度,春比之日东升,夏比之日中天,秋比之日沉落,冬比之日反背。如此,北斗七星行度已寓一年中气候与一日中温度之变化,同有寒暖燥湿的大小循环于其中,且又可明地理之方位所在。(春比:即比春,到春季时。其余同上)
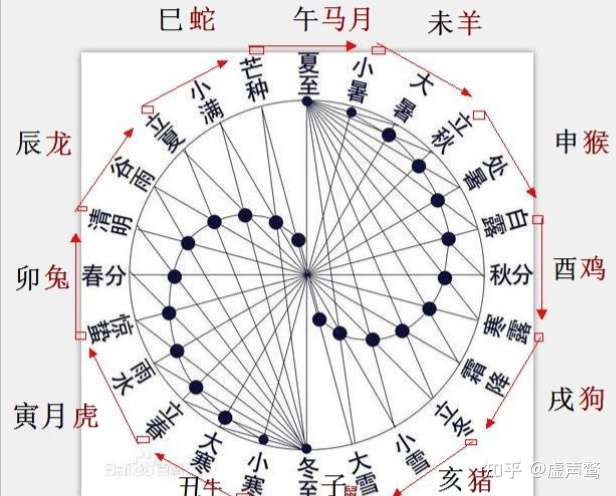
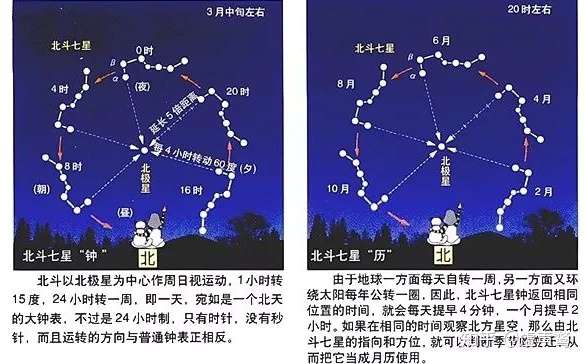
为什么要提及月建这一概念呢?读者可能发现,本文讲述农历的部分中,从开头到此处,并没有用诸如一月正月这样的称谓去命名一个朔望月。
出于一种惯常的思维,既然子位作为昼夜交替与寒暑交替的循环点,那把子月作为一岁的起点不就好了?但须知,历法是为指导人而产生的工具,具有强烈的历史与文化属性。
古代江山易主后,君主们为了昭告天下自己的正统地位,常常会适当改变前朝延续下来的一些社会传统,强调自己得位的正当性。而月建,自然也是改变的传统之一。
夫改正朔者,谓夏后氏建寅, 殷人建丑, 周人建子。 (正朔,月建也) ——《公卿以下冕服议》
我们先承认冬至必落在子月这个约定,然后可以得出下面的推论:
夏朝月建为寅月,且寅在十二支排行第三,所以夏历以寅月为正月,以此类推子月就是十一月。(冬月)
但若采用周正时,情况就完全不同。首先一年之定义在此情况下就与一岁的定义相同了,但此时子月就变成了一年的首月,而冬至又落在子月,所以一年的首个季节就是冬季,不符合人们对于新年大地回暖的认知。
以上可能是夏正更朔且建寅的原因之一。
从玄学一些的角度来说,丑在五行属土,而寅属木,木克土,周天子想借此来宣示自己的统治也是存在一定道理的。
回到正题,自夏正建寅之后,后世王朝便基本没有更改过月建,现在通行的农历依然采用夏正形式。
确立了月建为寅之后,我们可以很自然地把十二地支与十二个月对应起来。
即:
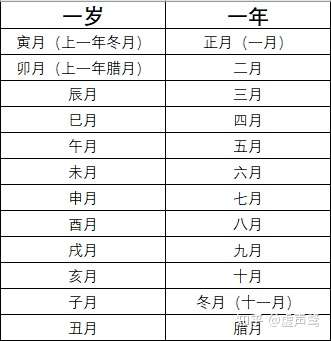
2.如何定月首
前文提到过,农历的月首必须严格地是一个朔日。
当天月球和太阳黄经相等,称为朔,月球运行到地球和太阳之间,和太阳几乎同时出没,在地球上是看不到月亮的。
当某一天是朔日时,当天晚上一定无法在地球上观测到月球,这是朔日的外在表现。
而核心是月球视黄经与太阳视黄经相等,这也是我们用以确定月首的方法。
只要计算出准确的朔日时刻,并向下取整到当天,则所得结果就是待求的朔日日期。
但因涉及计算内容,此处按下不表,将在下篇展示。
3.如何闰月
前文提到过,一个朔望月的平均长度约为29天12小时44分()。若一年设十二个朔望月,那么累计天数(
)将少于一个回归年的约365天5小时48分(
),久而久之就会出现系列文章(一)中儒略历的问题。(每年的误差时间达到
,这意味着每约18年农历季节都会与真实情况恰好相反)所以需要有一套置闰规则,使得历法能够合乎实际情况。
但无论置闰方法如何,都遵从十九年七闰的约定。
考虑置闰的目的本身,即让个朔望月的长度与
个回归年的长度恰好相配。
那么有:
简单变形有:
,那么平均一年需要闰
个月。
在实际生活中,我们习惯以整数来度量年长与越长,那么求解置闰的问题就可以进一步转化为:
对于若干年及这些年份需要闰的总月数
,求任意两个整数的商,使得这个商与
的比值较为接近。
include
include
int main()
{
for(float x=1;x<30;++x)
for(float y=1;y 精确度是最重要的,但其次也要考虑到操作的便利性。对于特别大的情况,虽然从比值接近程度上看更为适合,但是却难以执行(如下图,在
时,每87个回归年闰32个月似乎是更优解,但是这带来了更多的观测成本和时间成本)
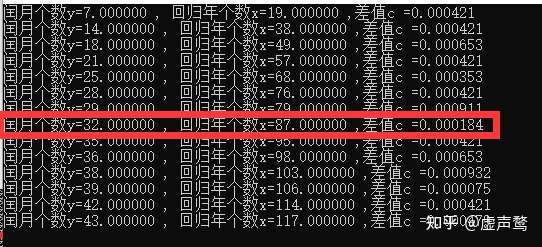
放宽范围的闰月个数y与年数x组合 看似选择很多,但仔细观察以后会发现,很多与
的组合实际上是之前组的线性相关组。
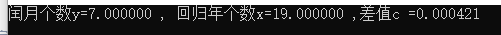
限制年数x小于30时的情况 很明显,综合多方面因素,选择十九年七闰是最优解。
但是,要如何把这七个月安排到十九年中呢?
这里需要再引入一个概念中气。
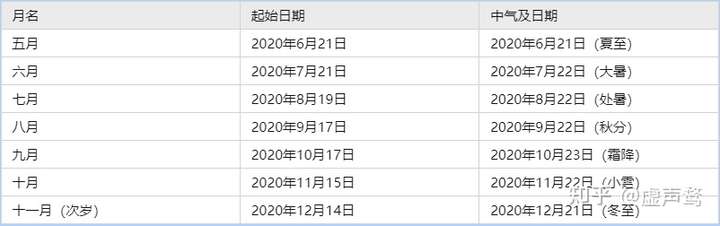
古代历法以二十四节气与农历十二个月相配,每月二气:在月初的叫节令,在月中以后的叫中气。如下图所示:
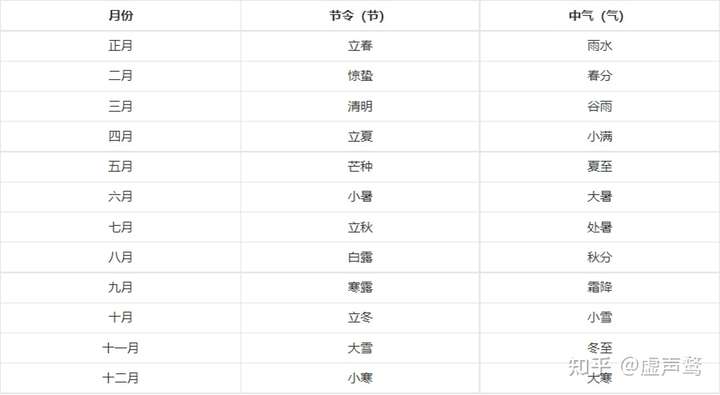
月名与节令/中气的对应关系 通过上文分析,我们知道,若不进行闰月,农历季节每隔一段时间都会和真实情况恰好反相。[1]那么如何衡量农历季节是否与真实情况相符呢?很显然就是用刚刚引入的中气了。
只要一个月不失却它的中气(换句话说,中气落在对应的那个月内),就认为是不需要闰月的。
因为一个农历年[2]短于一个回归年 ,那么随着时间推移,农历年的日期将会一直越前于回归年,直到农历年恰好比回归年快一整年,然后再重复这个过程。
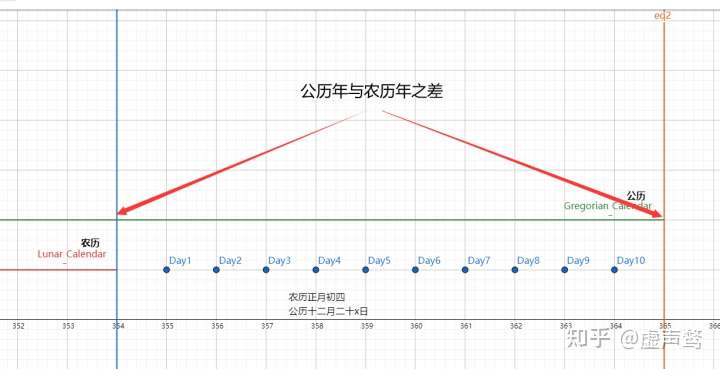
为了便于理解,假设二者在某一时刻有相同的起点,则公历年与农历年的一年分别如图所示。图中绿色线段代表一个公历年,红色线段代表一个农历年(此处的农历年取不闰月的情况,闰月的分析同上)。为10个离散点,分别表示介于农历第一年后与公历第一年内的10天。
以为例,该天为农历第二年正月初四,但却是公历第一年十二月二十日后的某一天。随着时间的推移,农历将会越来越超前公历。(二十四节气在公历的视角下日期只在数天范围内波动,因为二十四节气的本质是太阳视黄经到达15°的整数倍时对应的日期,所以超前公历也就是间接超前了实际的季节情况。)进而一个农历月的中气可能会落入该月的前一个月。
那么按照前文所述,这个月就是没有中气的。没有中气怎么办呢?首先想到的办法就是不改变这个月的月名,这样中气就会顺延到下一个月,从下一个月起再往下递增月名直至腊月(十二月)即可。但这样会导致一年多出一个朔望月,那顺理成章地我们就把这个月当作闰月,从而待闰的月数就减一。
具有以上基础,现在就可以着手试着编排一下农历了。
(注:这里的定气法和平气法准确来说并不是置闰的方法,仅仅只是方便深入研究所设标题)
Ⅰ、定气法
以公历2020年为例,利用下一章将提到的天文算法计算一下该年及上一年的二十四节气日期以及朔日时间表:


忽略略微有些混乱的年份前缀,只用保证朔日的次序与时刻、二十四节气的名称与时刻相配即可。
这里我们以岁为主体来进行编排,所以下面的结果是从公历2019年的冬月开始计算的。(至于为什么不以看起来更自然的年,后文会说明)
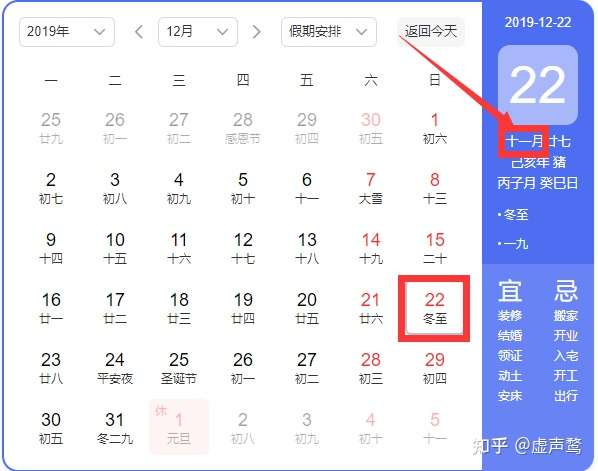
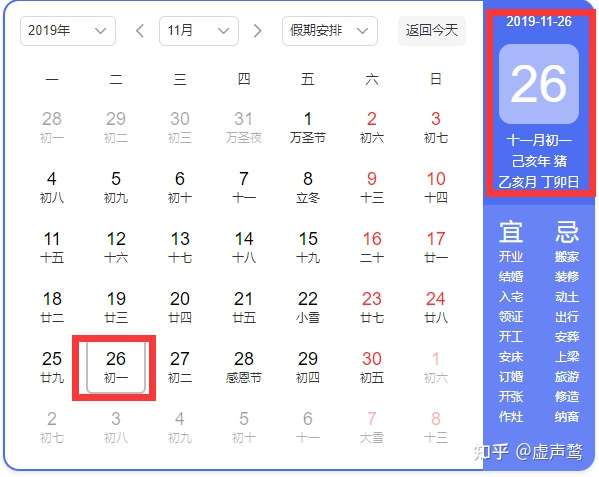
规则一:冬至日必须落在冬月内(实际上是冬至日决定冬月)
找到公历2019年的冬至日(2011年12月22日),那么冬至日所在的朔望月的名称就是冬月。
规则二:农历的月首严格与朔日重合
结合规则一,可以推出这个冬月的首日是冬至日前的第一个朔日,即2019年11月26日。换句话说,这一天是十一月初一。
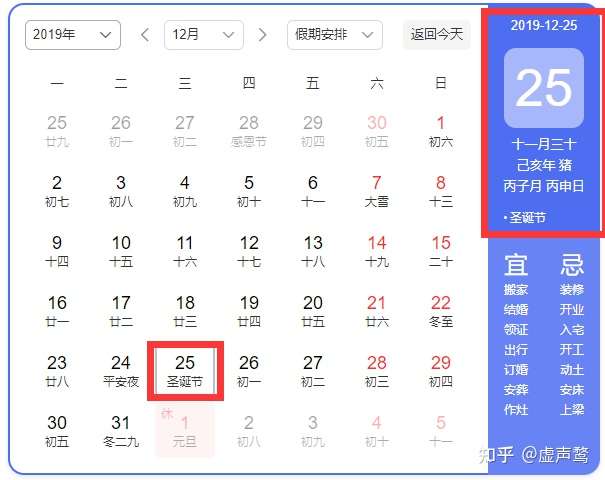
规则三:两个农历月之间以朔月为界
又据规则二之结论,容易知道这个冬月的最后一天是2011年12月25日。(下一个朔日的前一天)
十一月小,所以计算得出这个朔望月有天,所以这一天应为十一月三十日。(日数是从一开始计数的,故日名为间隔数+1)
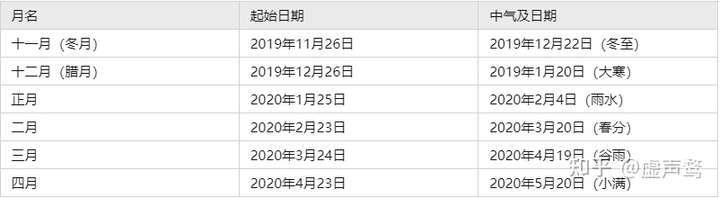
以此类推,可以得出如下结果:(夏正建寅,所以冬月就是十一月)
当继续填写五月的情况时,问题就出现了。
首先五月的中气为夏至日(6月21日),但是自冬月以来的第七个朔日也是6月21日。精确到小时看来,似乎这个中气应该算进上一个月里(夏至日为5:43,而同一天的朔日时刻为14:40),但我们仍将这个节气视为在新月中。[3](此处无关算法正确性或精确度的问题,是民间历法(也是现行历法)存在的缺陷导致了其与历理历法在置闰上的差异,若按照历理历法,此处不应当闰)
规则四:两冬至之间有12个整月辄该年闰,且闰第一个没有中气的月。若仅有11个整月就不闰。
正因为规则四的存在,我们计算农历时才需要从上一年的冬至开始。一年闰不闰取决于两个子月之间的关系,而与夏正建的寅月没有关系!
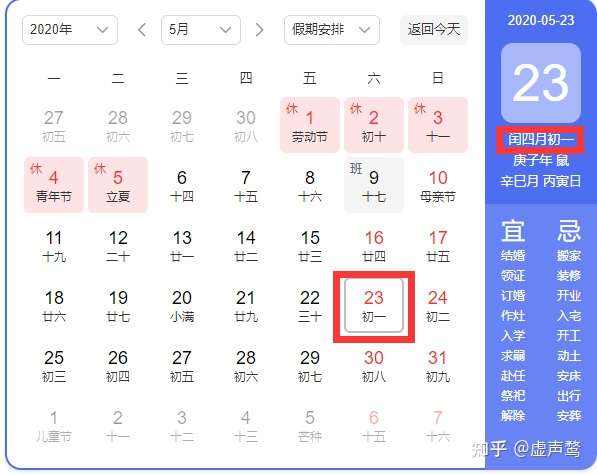
接上文,我们发现第五个月的中气落到了第五个月之外,并且该年有十二个整月。
根据规则需要将该月写作闰四月。

重复之前的工作,直至编排到下一岁的冬月前为止。
如此便是农历的整个编排过程。
顺带一提,大年没有三十是相当正常的现象。如果腊月首与下一个朔日之间只隔了29天,自然腊月最后一天就是大年二十九,不必为此大惊小怪。
一切似乎都很顺理成章的样子,那真的就没有任何地方值得商榷了吗?
并不是。读者应该注意到,确定二十四节气的时间在农历的制定中起到了决定性的作用。
恰恰是在如何确定节气的时间上,古代与现代有较大分歧。
①想法一:将一年的时间按节气平分。(每个节气的长度均=)
②想法二:将地球绕日公转的轨道角度按节气平分。
(每个节气的长度=)
看似没什么区别是吧?玄机正在此处!
我们来看一看地球绕日公转的示意图:
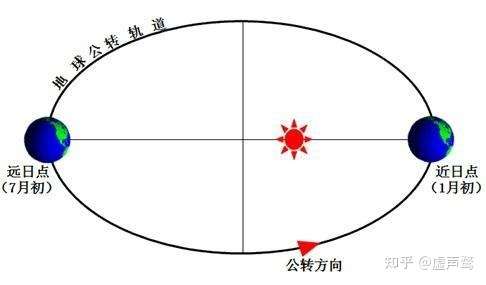
很明显,地球在一个椭圆轨道上运行。不考虑其他天体的影响,地球-太阳系统的角动量守恒,容易知道地球在近日点附近速度大小大于在远日点附近的速度大小,速度是随时间
改变的。
根据上述推理,我们可以推断,每个节气持续的时间一定不是简单的均分关系,事实上也的确如此。
在规则四中提到闰第一个没有中气的月的深意即在于此,如果以真实的二十四节气时间为参照,又规定每个没有中气的月都要闰的话,某些情况下会出现一年要闰两个月的情况。
本文编排农历采用了第二种办法(均分轨道角度),此称二十四节气的定气确定法。
古人并非没有意识到上述情况,但是如果要得出二十四节气的精确时间将需要大量精密的观测,这无疑是反社会条件的,因此在清代采用《时宪历》前,古人采用的都是平气法。
Ⅱ、平气法
平气法将一年的天数按照二十四节气等分为24份,那么每个节气的时长就为。从立春开始,每过约15.22日就交一个新的节气,此为平气法。(立春是一年的第一个节气,也是二十四节气之首)
按照这种规则计算出来的节气时间与实际存在一定出入。按照分析,平气法实际上是不合理的。
西汉成《太初历》即为一种平气历,在置闰上与现今使用的《时宪历》唯一的区别是,前者将闰月分插于一年中,并规定以每个无中气的月为闰月,沿用前月之月序。
并且两个冬至间有11个整月就不置闰,有12个整月闰前不闰后。
故在研究不同朝代间的历史时,要注意平气/定气带来的月名问题。
下篇将用全篇来讲述如何利用天文算法将指定的公历日期转换成农历日期。
参考
^每年的误差时间达到 10.875d ,这意味着每约18年农历季节都会与真实情况恰好相反^农历年可以简单地理解为12或13个朔望月组成的一年^新中国成立以后没有颁布新的官方农历历法,将历法和政治分离体现了时代的进步,但是由于没有 官方历法,也引起了一些问题。比如我国现在采用的农历历法是《时宪历》,它源于清朝顺治年间(公元1645)颁布的《顺治历》,它有两个不足之处:一个是日月合朔和节气的时间以北京当地时间为准,也就是东经116度25分的当地时间,其节气和新月的观察只适用于中原地区。其它经度的地方,因为时间的关系,对导致日月合朔和节气时间的差异导致置闰和月顺序各不相同。另一个不足之处就是日月合朔时间和节气时间判断不精确,如果日月合朔时间和节气时间在同一天,不管具体的时间是否有先后,一律将此节气算做新月中的节气,这样一来,如果这个节气是中气,就会影响到闰月的设置。历理历法针对这两点进行了改进,对节气时间和日月合朔时间统一采用东经120度即东八区标准时,这样在任何时区的节气和置闰结果都是一样的,以东八区标准时为准。对于节气时间和日月合朔时间在同一天的情况,精确计算到时、分、秒,只有日月合朔时间在节气时间之前,这个节气才包含在次月内。历理历法从理论上讲更符合现代天文学的精确计算,但是需要注意的是,历理历法仍然只是存在于理论上的历法,我国现行的农历历法依然是民间历法《时宪历》或《顺治历》。https://orbit.blog.csdn.net/article/details/9337377
